Mass in Special Relativity: ভরের আপেক্ষিকতা কি সত্যি?

লেখাটি বিজ্ঞানব্লগে 'বিশেষ আপেক্ষিকতার বিশেষ ভর: আপেক্ষিক ভর কি সত্যি?' শিরোনামে প্রকাশিত।

(The English version of the article is also available.)

----------------------------------------------------

বস্তুর বেগ কখনোই আলোর বেগের সমান হতে পারে না - এ কথাটা আমরা সবাই কম বেশি জানি। স্পেশাল রিলেটিভিটির (বিশেষ আপেক্ষিকতা) জ্ঞান না থাকলেও জনপ্রিয়ধারার বিজ্ঞান কন্টেন্টের প্রভাবে কৌতূহলী পাঠকদের কাছে এটা আর অজানা নয়। স্বাভাবিক ভাবেই তাদের অনেকের মনে প্রশ্ন জাগে কেন বস্তুর বেগ আলোর বেগের সমান হতে পারে না? আর একটু ঘাটতেই তারা চট করে পেয়ে যায় একটা প্রচলিত ব্যাখ্যা এবং তাতে সন্তুষ্ট হয়ে যায়। সেই ব্যাখ্যাটা সহজ কথায় এরকমঃ "বস্তুর ভর আপেক্ষিক। বেগ বাড়ার সাথে সাথে তার ভরেরও পরিবর্তন হয়। তাই কেউ যদি বস্তুর উপর বল প্রয়োগ করে করে বেগ বাড়াতে বাড়াতে আলোর বেগের কাছাকাছি যাওয়ার চেষ্টা করে, সে দেখবে বেগ না বেড়ে ভর বেড়ে যাচ্ছে।" তো এই ব্যাখ্যার ভিত্তি 'আপেক্ষিক ভর' বিষয়টা কতটুকু যৌক্তিক? গতির জন্য বস্তুর ভর কি সত্যিই পরিবর্তন হয়?

(ভরের আপেক্ষিকতা - কার্টুন ছবিটি ইউটিউব চ্যানেল minutephysics থেকে অনুপ্রাণিত)

স্পেশাল রিলেটিভিটির ধারণা প্রথম প্রকাশিত হয়েছিল সেই ১৯০৫ সালে। মাঝে শত বছরের বেশি পেরিয়ে গিয়েছে। কাল দীর্ঘায়ন, দৈর্ঘ্য সংকোচনের পাশাপাশি ভর বৃদ্ধির কথাও তো স্পষ্টভাবে বলা থাকে জনপ্রিয়বিজ্ঞানের বিভিন্ন লেখালেখিতে, এইচএসসির পদার্থবিজ্ঞান বইয়ে, স্নাতক পর্যায়ের অনেক পাঠ্যবইতে। তাহলে আপেক্ষিক ভরের বিষয়ে যৌক্তিকতা বা অযৌক্তিকতার প্রশ্ন আসছে কেন?

আসলে শুরুর দিকে আপেক্ষিকতার বিভিন্ন ধারণা খোদ আইনস্টাইন-সহ তৎকালীন পদার্থবিদেরা ঠিকমত বুঝতে পারেননি। তেমনই একটা সেকেলে ধারণা হচ্ছে আপেক্ষিক ভর। এই ধারনাটা পরিষ্কার ভাবে বুঝতে বেশ কিছু সময় লেগেছে। কিন্তু ততদিনে তা পাঠ্যপুস্তকে স্থান পেয়ে গিয়েছিল। পুরান বইয়ে থাকা সেই স্থির-ভর, গতিশীল-ভর এর কনভেনশনটাই পরের প্রজন্মের বইগুলো অনুসরণ করতে থাকে। এবং বর্তমানের অনেক পাঠ্যবইয়ে সেই অনুসরণ এখনো চলমান। কারণ সেইসব বই-লেখকদের মতে, এটা ব্যবহার করে ইন্ট্রোডাক্টরি পর্যায়ে রিলেটিভিটি বোঝানো সহজ হয়। প্রজন্মের পর প্রজন্ম শিক্ষার্থী, শিক্ষক, লেখকদের মধ্যে এই ধারণাটি এমনভাবে গেথে গিয়েছে যে এটাকে আখ্যা দেওয়া হয়েছে pedagogical virus হিসেবে। যাই হোক, পদার্থবিদেরা যারা বর্তমানে প্রফেশনালি আপেক্ষিকতা নিয়ে কাজ করেন, তারা কিন্তু কেউ আর স্থির-ভর, গতিশীল-ভর টার্মগুলো ব্যবহার করেন না। তাদের নতুন কনভেনশন অনুসারে ভর দুইরকম নয়, বরং একটাই। আগের কনভেশনে স্থির ভর বলতে যা বোঝানো হতো, সেটাই হল একমাত্র ভর। রিলেটিভিটির আধুনিক পাঠ্যবইগুলোতে আপনারা এই নতুন কনভেনশনই দেখতে পাবেন। বার বার 'নতুন কনভেনশন' বলায় ভেবে বসবেন না যে ভরের ধারণার এই পরিবর্তন হয়েছে সাম্প্রতিক। তা কিন্তু নয়, বরং এই নতুন কনভেনশন পদার্থবিদেরা ব্যবহার করে আসছেন গত অর্ধ শতক ধরে।

আজকের এই লেখায় আমরা গাণিতিক ভাবে দেখব কিভাবে ভর অপরিবর্তনশীল থাকে। দেখব কেন আপেক্ষিক ভরের ধারণাটা আনা হল; সেই সাথে এই ধারণার অসুবিধা বা অযৌক্তিকতাও কিছুটা দেখার চেষ্টা করব এই লেখায়। চলুন শুরু করা যাক। লেখাটিকে তিনটা সেকশনে ভাগ করেছিঃ

• ভেক্টর এবং স্থানাংক পরিবর্তন
• বিশেষ আপেক্ষিকতায় ভর
• আপেক্ষিক ভরের অবতারণা

পাঠকদের প্রতি অনুরোধ রইল, কোন সেকশন বাদ না দিয়ে পুরোটুকু পড়বেন। লেখায় গণিত আছে বিধায় অনেক পাঠক হয়তো শুরুতেই আগ্রহ হারিয়ে ফেলতে পারেন। কিন্তু যদি পদার্থবিজ্ঞানে সত্যিকার আগ্রহ থাকে, তাহলে গণিতে অনীহা কাম্য নয়। গণিত লুকিয়ে পদার্থবিদ্যার এই বিষয়গুলো চর্চার একটা প্রবণতা দেখা যায়। ভাসা ভাসা জ্ঞান নিয়েও অনেকে এসব বিষয়ে illusory superiority (Dunning-Kruger effect) অনুভব করেন। প্রয়োজনীয় গণিত থাকলে এই প্রভাব কিছুটা কমানো যাবে, আশা করছি।

ভেক্টর এবং স্থানাংক পরিবর্তন

বিশেষ আপেক্ষিকতার গণিতে যাওয়ার আগে চলুন প্রথমে ভেক্টর এবং কোঅর্ডিনেট (স্থানাংক) পরিবর্তনে ভেক্টরের স্বরূপ কেমন হয় সেবিষয়গুলো রিভিউ করে আসি।

ধরা যাক, একটা ভেক্টর, ঠিক করে বললে পজিশন ভেক্টর হল $\overrightarrow{X}$। এটাকে একটা দ্বিমাত্রিক কার্টেশিয়ান কোঅর্ডিনেটে থেকে আমরা লিখি এভাবেঃ

$$\overrightarrow{X}=(x,y)=x\hat{ı}+y\hat{ȷ}$$

এখানে বেসিস ভেক্টর $\hat{ı},\hat{ȷ}$ দিয়ে না লিখে $\hat{x},\hat{y}$ অথবা ${\overrightarrow{e}}_x,{\overrightarrow{e}}_y$ দিয়েও লিখতে পারি।

$$\overrightarrow{X}=x\hat{x}+y\hat{y}=x{\overrightarrow{e}}_x+y{\overrightarrow{e}}_y$$

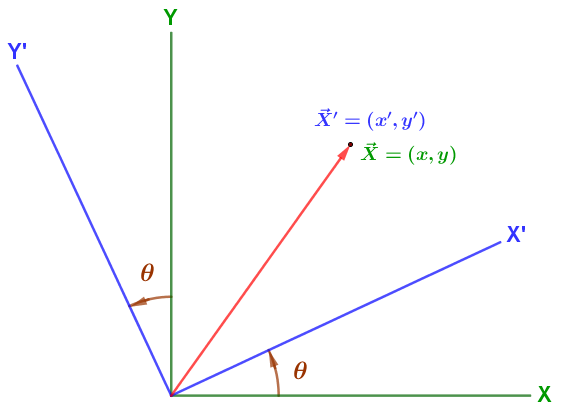
এখন আরেকটা কোঅর্ডিনেটের কথা চিন্তা করা যাক যেটা আগেরটার সাপেক্ষে ঘড়ির-কাটার বিপরীত দিকে $\theta$ কোণে ঘুরানো। এই নতুন কোঅর্ডিনেটে থেকে একই ভেক্টর $\overrightarrow{X}$ কে লেখা যায়ঃ $${\overrightarrow{X}}^{\prime }=x^{\prime }{\overrightarrow{e}}_x^{\prime }+y^{\prime }{\overrightarrow{e}}_y^{\prime }$$

X-Y এবং X'-Y' কোঅর্ডিনেটে ভেক্টরটির উপাংশ $(x,y)$ এবং $(x^{\prime },y^{\prime })$ এর মধ্যকার সম্পর্কঃ

$$\begin{array}{rl}{x}^{\prime }& =x\cos \theta +y\sin \theta \\ y^{\prime }& =-x\sin \theta +y\cos \theta \end{array}$$

এই বিষয়টা ভেক্টরটাকে ঘড়ির-কাটার দিকে $\theta$ কোণে ঘুরিয়ে পরিমাপ করার সমতুল্য। যাইহোক, এই সমীকরণদ্বয়কে ম্যাট্রিক্স আকারে লিখলে দাঁড়ায়ঃ

$$\begin{array}{rl}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\\ ⟹X^{\prime }& =RX\end{array}$$ যেখানে, $R=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)$ হল 2D রোটেশন ম্যাট্রিক্স।

এ তো গেল ভেক্টরের উপাংশ পরিবর্তনের কথা। উপাংশের পাশাপাশি বেসিস ভেক্টর পরিবর্তন হয়।
ছবিটা খেয়াল করলে বুঝতে পারবেন, কোঅর্ডিনেট পরিবর্তনে ভেক্টরেরটির হিসাব করা উপাংশ আর বেসিস ভেক্টরের পরিবর্তন এসেছে ঠিকই। কিন্তু ভেক্টরটা নিজে কি সাইজে ছোট-বড় হয়েছে? হয় নি। চলুন দেখি ভেক্টরের নিজের সাইজ যে একই থাকছে সেটা গাণিতিকভাবে প্রকাশ করা যায় কি না।
আমরা জানি, ভেক্টরের নর্ম বা দৈর্ঘ্য একটা স্কেলার রাশি।

X-Y কোঅর্ডিনেটে আমাদের আলোচিত পজিশন ভেক্টরের দৈর্ঘ্য হলঃ $$\begin{array}{rl}||\overrightarrow{X}||& =\sqrt{x^2+y^2}\\ ⟹||\overrightarrow{X}|{|}^2& =x^2+y^2\end{array}$$ আর X'-Y' কোঅর্ডিনেটে ভেক্টরটির দৈর্ঘ্যঃ $$\begin{array}{rl}||{\overrightarrow{X}}^{\prime }||& =\sqrt{{x^{\prime }}^2+{y^{\prime }}^2}\\ ⟹||{\overrightarrow{X}}^{\prime }|{|}^2& =(x\cos \theta +y\sin \theta {)}^2+(-x\sin \theta +y\cos \theta {)}^2\\ ⟹||{\overrightarrow{X}}^{\prime }|{|}^2& =x^2+y^2\end{array}$$

তার মানে বুঝতে পারছেন, কোঅর্ডিনেট ঘুরানোর জন্য ভেক্টরের দৈর্ঘ্যে কোন পরিবর্তন হয় নি। অর্থাৎ রোটেশনের সাপেক্ষে ভেক্টরের দৈর্ঘ্য ইনভ্যারিয়েন্ট (অপরিবর্তনশীল)। এই ভেক্টর দৈর্ঘ্যকে আরেকভাবে প্রকাশ করা যায়, সেটা হল ভেক্টরটির নিজের সাথে নিজের স্কেলার বা ডট গুণন (এটা ভেক্টর-দৈর্ঘ্যের বর্গের সমান)।

$||\overrightarrow{X}|{|}^2=||{\overrightarrow{X}}^{\prime }|{|}^2=\overrightarrow{X}\cdot \overrightarrow{X}=$ ইনভ্যারিয়েন্ট স্কেলার প্রডাক্ট

দৈর্ঘ্যের চেয়ে এই স্কেলার গুণন ফর্মটাই আমাদের জন্য বেশি ব্যবহার উপযোগী হতে চলেছে।

এতক্ষন আমরা দ্বিমাত্রিক ভেক্টর বা 2-ভেক্টর দিয়ে কথা বললাম। এগুলো আমাদের ত্রিমাত্রিক ভেক্টর বা 3-ভেক্টরের জন্য সত্যি। 3-পজিশন ভেক্টরকে লিখি এভাবেঃ $$\begin{array}{rl}\overrightarrow{X}& =(x,y,z)\\ & =x{\overrightarrow{e}}_x+y{\overrightarrow{e}}_y+z{\overrightarrow{e}}_z\\ & =X^1{\overrightarrow{e}}_1+X^2{\overrightarrow{e}}_2+X^3{\overrightarrow{e}}_3\\ & =(X^1,X^2,X^3)\end{array}$$ রিলেটিভিটিতে $(x,y,z)$ না লিখে $1,2,3$ ইন্ডেক্স দিয়ে $(X^1,X^2,X^3)$ আকারেও লেখা হয়। তাই আপনাদের অবগতির জন্য এই নোটেশনও লিখে রাখলাম।
তো কোঅর্ডিনেট ঘোরানোর আলোচনাটি 3-পজিশন ভেক্টরের জন্য সারমর্ম করলে দাঁড়ায়

ভেক্টরটির উপাংশঃ $X^i\leftarrow$ (পরিবর্তন বা রূপান্তর) $\to X^{\prime j}$, যেখানে $i,j=1,2,3$
রোটেশনের সাপেক্ষে ইনভ্যারিয়েন্টঃ $\overrightarrow{X}\cdot \overrightarrow{X}=x^2+y^2+z^2$

বিশেষ আপেক্ষিকতায় ভর

স্পেশাল রিলেটিভিটির আলোচনা চতুর্মাত্রিক স্থানকাল নিয়ে। এখানে বস্তু যে পথে ভ্রমণ করে, সেটা হল তার ওয়ার্ল্ড লাইন। বস্তুর এই অবস্থান, গতির ব্যাখ্যার আমাদের দরকার চারমাত্রিক ভেক্টর বা 4-ভেক্টর বা মিনকোস্কি ভেক্টর। এটা আমাদের পরিচিত 3-ভেক্টরের মতই, সাথে অতিরিক্ত যোগ হয় সময় অক্ষ বরাবর ভেক্টর-উপাংশ, কারণ স্থানের মত সময়ও একটা মাত্রা।

3-ভেক্টরে ছিল 3টা উপাংশ $X^i$ যেখানে $i=1,2,3$। মানে $(X^1,X^2,X^3)=(x,y,z)$।

আর এখানে 4-ভেক্টরে 4 টা উপাংশ $X^{\mu }$, যেখানে $\mu =0,1,2,3$। এই $\mu =0$ দিয়ে নির্দেশ করছি সময় বরাবর উপাংশ। বাকি তিনটা ($\mu =1,2,3$) দিয়ে নির্দেশ করছি স্থানের তিনটা উপাংশকে যারা 3-ভেক্টরের বেলায় $i=1,2,3$ দিয়ে নির্দেশিত ছিল।
মানে এখানে $(X^0,X^1,X^2,X^3)=(t,x,y,z)$।

বলে রাখি, আমি ন্যাচারাল ইউনিটে লিখছি। ন্যাচারাল ইউনিটে ($c=1$ ধরে) আমরা 4-পজিশন ভেক্টরকে লিখতে পারি এভাবেঃ $$\begin{array}{rl}\mathbb{X}& =(X^0,X^1,X^2,X^3)\\ & =(t,x,y,z)\\ & =t{\overrightarrow{e}}_t+x{\overrightarrow{e}}_x+y{\overrightarrow{e}}_y+z{\overrightarrow{e}}_z\end{array}$$

ভেক্টর রিভিউ অংশে আমরা দ্বিমাত্রিক কোঅর্ডিনেট রোটেশনে কিভাবে ভেক্টর উপাংশ পরিবর্তন হয় সেটা দেখে এসেছি। এখানে আমরা 4-ভেক্টর উপাংশ পরিবর্তন দেখব লরেন্টজ রূপান্তর এর প্রেক্ষিতে। এটাও এক ধরনের চারমাত্রিক কোঅর্ডিনেট রোটেশন বলতে পারেন। তবে পুরোপুরি এক জিনিস নয়।

লরেন্টজ রূপান্তরে 4-পজিশন ভেক্টরের সম্পর্ককে লেখা যায় এরকমঃ
ভেক্টরটির উপাংশঃ $X^{\mu }\leftarrow$ (লরেন্টজ রূপান্তর) $\to X^{\prime \nu }$, যেখানে $\mu ,\nu =0,1,2,3$
ম্যাট্রিক্স আকারেঃ $X^{\prime }=\mathrm{\Lambda }X$
এখানে $\mathrm{\Lambda }$ হল লরেন্টজ ট্রান্সফর্মেশন ম্যাট্রিক্স। $$\mathrm{\Lambda }=\left(\begin{array}{cccc}\gamma & -\beta \gamma & 0& 0\\ -\beta \gamma & \gamma & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$ এই ম্যাট্রিক্স x অক্ষ বরাবর আপেক্ষিক গতিতে চলমান দুইটা ফ্রেমের কোঅর্ডিনেট রূপান্তরকে প্রকাশ করে।

এখানে আপেক্ষিক গতি $=v$ এবং লরেন্টজ সহগ $\gamma =\frac{1}{\sqrt{1-{\beta }^2}}$ যেখানে $\beta =\frac{v}{c}$। ন্যাচারাল ইউনিটে থাকতে চাচ্ছি। তাই এগুলোতে $c=1$ বসালাম, $\beta =v$, $\gamma =\frac{1}{\sqrt{1-v^2}}$।

কিছুক্ষণ আগে আমরা দেখলাম, 2D কোঅর্ডিনেট রোটেশনে 2-ভেক্টরের ডট প্রডাক্ট পরিবর্তন হয় না। একইভাবে 4-ভেক্টরের ডট প্রডাক্টও পরিবর্তন হয় না লরেন্টজ রূপান্তরে। আর যেহেতু এটার ফলাফল একটা স্কেলার রাশি এবং লরেন্টজ রূপান্তরে অপরিবর্তনশীল, এটার আরেক নাম লরেন্টজ স্কেলার। মানে যেকোন 4-ভেক্টরের দৈর্ঘ্য হল একটা লরেন্টজ স্কেলার।

এখন চলুন দেখা যাক আমাদের এই 4-ভেক্টরের ডট প্রডাক্ট কিভাবে লেখা হয়। ডট প্রডাক্ট, $$\begin{array}{rl}{X}_{\mu }{X}^{\mu }& =(X^0{)}^2-(X^1{)}^2-(X^2{)}^2-(X^3{)}^2\\ & =(t{)}^2-(x{)}^2-(y{)}^2-(z{)}^2\\ & =t^2-r^2\end{array}$$

এই প্রডাক্টের একটা নাম আছে, একে বলে স্পেসটাইম ইন্টারভাল। এর থেকে সহজে যথার্থ সময়, সময় সম্প্রসারণের বিষয়গুলো আনা যায়। সে আলোচনায় যাচ্ছি না আজ।

আর এখানে ডট প্রডাক্টে নেগেটিভ সাইন কিভাবে আসল তা জানতে 4-ভেক্টরের ডট প্রডাক্ট কিভাবে করতে হয়, সেটা বুঝতে হবে। এখানে ব্যবহার করা মেট্রিক ম্যাট্রিক্সের বিষয়টা জানতে হবে। এটার দুইরকম কনভেনশন আছে, এই কনভেনশনকে বলা হয় মেট্রিক সিগনেচার। একটা হল $(-,+,+,+)$, আরেকটা হল $(+,-,-,-)$।

সহজ করে বলতে চাইলে, আমরা আমাদের 3-ভেক্টরের বেলায় আমরা ব্যবহার করি $\hat{ı}\cdot \hat{ı}=\hat{ȷ}\cdot \hat{ȷ}=\hat{k}\cdot \hat{k}=1$ বা আরেক ভাবে লিখলে ${\overrightarrow{e}}_x\cdot {\overrightarrow{e}}_x={\overrightarrow{e}}_y\cdot {\overrightarrow{e}}_y={\overrightarrow{e}}_z\cdot {\overrightarrow{e}}_z=1$। 4-ভেক্টরের ক্ষেত্রে $(-,+,+,+)$ সিগনেচারের বেলায় এদের সাথেই যুক্ত হয় ${\overrightarrow{e}}_t\cdot {\overrightarrow{e}}_t=-1$।

অন্যদিকে $(+,-,-,-)$ সিগনেচারে কনভেনশনটা বিপরীত। মানে সেক্ষেত্রে ${\overrightarrow{e}}_t\cdot {\overrightarrow{e}}_t=1$ এবং ${\overrightarrow{e}}_x\cdot {\overrightarrow{e}}_x={\overrightarrow{e}}_y\cdot {\overrightarrow{e}}_y={\overrightarrow{e}}_z\cdot {\overrightarrow{e}}_z=-1$। সময় অক্ষ থেকে স্থানের অক্ষগুলোকে আলাদাভাবে চিহ্নিত করতে এই বিপরীত সাইন আনা। পদার্থবিজ্ঞানের ভিন্ন ভিন্ন শাখায় এই দুইরকম সিগনেচারেরই চাহিদা আছে। আজকের এই লেখাটির প্রেক্ষিতে আমি ব্যবহার করেছি এই $(+,-,-,-)$ সিগনেচার।

গাণিতিক কচকচানি বোধ হয় বেশি হয়ে যাচ্ছে, কিন্তু এগুলো প্রয়োজন ছিল। এই গাণিতিক বিষয়গুলো আরো ভালভাবে শিখতে আগ্রহী পাঠকেরা তথ্যসূত্রে উল্লেখিত বইগুলো দেখতে পারেন। এখন চলুন মূল আলোচনায় ফেরা যাক।

আইনস্টাইনের বিখ্যাত ভর-শক্তি সমতা ন্যাচারাল ইউনিটে লিখতে পারিঃ $$\begin{array}{rl}{E}^2& =m^2+p^2\\ \text{(১)}& ⟹m^2& =E^2-p^2\end{array}$$ বিশেষ আপেক্ষিকতার আলোচনায় সরণ, বেগ, ভরবেগ, ত্বরণ সবই 4-ভেক্টর। তো চতুর্মাত্রিক ভরবেগ বা 4-মোমেন্টামকে লেখা যায় এভাবেঃ $$\begin{array}{rl}\mathbb{P}& =E{\overrightarrow{e}}_t+P^x{\overrightarrow{e}}_x+P^y{\overrightarrow{e}}_y+P^z{\overrightarrow{e}}_z\\ & =E{\overrightarrow{e}}_t+\overrightarrow{p}\end{array}$$ এই ভেক্টরের উপাংশগুলোকে ম্যাট্রিক্স ফর্মে লিখলে দাঁড়ায়, $$P^{\mu }=\left(\begin{array}{c}{P}^0\\ P^1\\ P^2\\ P^3\end{array}\right)=\left(\begin{array}{c}{P}^t\\ P^x\\ P^y\\ P^z\end{array}\right)=\left(\begin{array}{c}E\\ P^x\\ P^y\\ P^z\end{array}\right)=\left(\begin{array}{c}E\\ p\end{array}\right)$$ তো কিছুক্ষণ আগে দেখলাম 4-পজিশনের স্কেলার প্রডাক্ট কেমন হয়। একইভাবে 4-মোমেন্টামের স্কেলার প্রডাক্ট দেখাতে পারিঃ $$\begin{array}{rl}{P}_{\mu }{P}^{\mu }& =(P^0{)}^2-(P^1{)}^2-(P^2{)}^2-(P^3{)}^2\\ \text{(২)}& & =E^2-p^2\end{array}$$ এখন সমীকরণ $\text{(১)}$ আর $\text{(২)}$ তুলনা করে দেখা যাচ্ছে, $$\begin{array}{}\text{(৩)}& m^2=P_{\mu }{P}^{\mu }\end{array}$$

তাহলে ঘটনা কী দাঁড়াচ্ছে! আপনারা বুঝতে পারছেন, স্কেলার গুণন $P_{\mu }{P}^{\mu }$ লরেন্টজ রূপান্তরে অপরিবর্তীত থাকে। আর সেটাই হচ্ছে ভর। ঠিক করে বললে, ভর হল 4-মোমেন্টামের দৈর্ঘ্য।

ভরের যদি লরেন্টজ রূপান্তর সম্ভব হতো, তাহলে তাকে তো এরকম স্কেলার গুণন আকারে প্রকাশ করা যেত না। তাহলে আমরা দেখতে পাচ্ছি, তিনমাত্রিক কোঅর্ডিনেট রোটেশনে একটা 3-ভেক্টরের দৈর্ঘ্য যেভাবে ইনভ্যারিয়েন্ট থাকে, তেমনিভাবে চারমাত্রিক লরেন্টজ রূপান্তরে ইনভ্যারিয়েন্ট (লরেন্টজ স্কেলার) থাকছে বস্তুর ভর।

আপেক্ষিক ভরের অবতারণা

এই পর্যায়ে আপনি প্রশ্ন করতে পারেন - ভর যদি ইনভ্যারিয়েন্ট বা লরেন্টজ স্কেলার হয়, তবে বইতে যে ভরের আপেক্ষিকতা দেখানো এভাবেঃ

$$m_{\text{rel}}=\frac{m}{\sqrt{1-\frac{v^2}{c^2}}}=\gamma m$$ এটা কিভাবে হল? চলুন দেখা যাক।

আমরা আগের আলোচিত লরেন্টজ রূপান্তর ম্যাট্রিক্স দিয়েই বিষয়টা দেখব। ধরছি, দুইটা ফ্রেম S এবং S' একটা আরেকটার সাপেক্ষে x অক্ষ বরাবর নির্দিষ্ট $v$ বেগে চলমান। তাহলে, দুই ফ্রেম থেকে হিসাব করা 4-মোমেন্টামের সম্পর্ককে ম্যাট্রিক্স আকারে আমরা লিখতে পারিঃ

$$\begin{array}{rl}{P}^{\prime }& =\mathrm{\Lambda }P\\ ⟹\left(\begin{array}{c}{E}^{\prime }\\ P^{\prime x}\\ P^{\prime y}\\ P^{\prime z}\end{array}\right)& =\left(\begin{array}{cccc}\gamma & -\beta \gamma & 0& 0\\ -\beta \gamma & \gamma & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}E\\ P^x\\ P^y\\ P^z\end{array}\right)\end{array}$$ সমীকরণগুলো আলাদা করে পাইঃ $$\begin{array}{rl}\text{(৪)}& E^{\prime }& =\gamma (E-\beta P^x)\text{(৫)}& P^{\prime x}& =\gamma (-\beta E+P^x)P^{\prime y}& =P^y\\ P^{\prime z}& =P^z\end{array}$$ যেহেতু আপেক্ষিক গতি শুধু x অক্ষ বরাবর, তাই $P^{\prime y}=P^y=0$ এবং $P^{\prime z}=P^z=0$।

এখন যেকোন একটা ফ্রেমকে বস্তুর গতির সাপেক্ষে রেস্ট ফ্রেম ধরে যাক। ধরলাম, S' ফ্রেম হচ্ছে সেই রেস্ট ফ্রেম। তাহলে, এই ফ্রেমে $P^{\prime x}=0$ এবং $\text{(১)}$ অনুসারে শক্তিঃ $$\begin{array}{rl}(E^{\prime }{)}^2& =m^2+(P^{\prime x}{)}^2\\ ⟹(E^{\prime }{)}^2& =m^2+0\\ \text{(৬)}& ⟹E^{\prime }& =m\end{array}$$

$\text{(৪)}$ থেকে পাইঃ $$\begin{array}{rl}m& =\gamma (E-\beta P^x)\\ ⟹E& =\frac{m}{\gamma }+\beta P^x\end{array}$$ $\text{(৫)}$ থেকে পাইঃ $$\begin{array}{rl}& 0=\gamma (-\beta E+P^x)\\ ⟹& P^x=\beta E\\ ⟹& P^x=\beta (\frac{m}{\gamma }+\beta P^x)\\ ⟹& (1-{\beta }^2)P^x=\beta \frac{m}{\gamma }\\ ⟹& \frac{P^x}{{\gamma }^2}=v\frac{m}{\gamma }\\ ⟹& P^x=\gamma mv\\ \text{(৭)}& \therefore & \overrightarrow{p}=\gamma m\overrightarrow{v}\end{array}$$

মূল পয়েন্ট এসে গিয়েছি আমরা। এখানে দেখা যাচ্ছে, 3-ভরবেগের সূত্রে $mv$ এর সাথে লরেন্টজ সহগ $\gamma$ গুণ আকারে আছে। কিন্তু নিউটনিয়ান মেকানিক্সে ভরবেগের সংজ্ঞায় আমরা দেখে এসেছি, $$\begin{array}{}\text{(৮)}& \overrightarrow{p}=m\overrightarrow{v}\end{array}$$ তাই পরিচিত নিউটনিয়ান ভরবেগের সাথে মিল রাখতে তৎকালীন অনেক পদার্থবিদেরা সমীকরণ $\text{(৭)}$ কে লিখেছিলেন এভাবেঃ $$\begin{array}{}\text{(৯)}& \overrightarrow{p}=m_{\text{rel}}\overrightarrow{v}\end{array}$$ আর এটা করতে গিয়ে আনা হয়েছিল ভরের একটা নতুন সংজ্ঞা - পরিবর্তনশীল ভর বা আপেক্ষিক ভরঃ $$\begin{array}{}\text{(১০)}& m_{\text{rel}}:=\gamma m\end{array}$$ এই নতুন ডেফিনিশন উপস্থাপনের ফলে একটা সুবিধা পাওয়া গেল। রিলেটিভিস্টিক 3-ভরবেগ 'দেখতে' নিউটনিয়ান ভরবেগের মত হয়ে গেল।

কিন্তু এটার ব্যবহারে বিপত্তি বা অসুবিধা আছে ঢের। স্পেশাল রিলেটিভিটি আর নিউটনিয়ান মেকানিক্সে তাৎপর্যপূর্ণ পার্থক্য আছে। তাই ভরবেগের পুরাতন সূত্রের সাথে মিল আনতে এখানে ভরের নতুন আরেকটা ডেফিনিশন আনা উপযোগী আইডিয়া নয়। $\overrightarrow{p}=m\overrightarrow{v}$ শুধু অল্প গতিতে চলা ভারী বস্তুর জন্য খাটে। আর যে সংজ্ঞাটা সবজায়গায় খাটে, সেটা জড়তার সাথে সম্পর্কিত। মানে ভরবেগ হল সেই জিনিসটা যার পরিবর্তনের হার হচ্ছে ফোর্স। আর $m_{\text{rel}}$ দিয়ে ভরবেগের দুইরকম স্বরূপ $\text{(৭)}$ ও $\text{(৮)}$ কে জোর করে মিলানো গেল ঠিকই। কিন্তু অন্যান্য টার্মের ক্ষেত্রে ক্লাসিকাল মেকানিক্সের সাথে রিলেটিভিটির সেই মিল আনতে এটা ব্যর্থ হয়। মানে $m_{\text{rel}}$ দিয়েও তারা 'দেখতে' একই হয় না। যেমন, $\overrightarrow{F}$ এর হিসাবটা দেখুনঃ $$\begin{array}{rl}\overrightarrow{F}& =\frac{d\overrightarrow{p}}{dt}\\ & =\frac{d}{dt}(m_{\text{rel}}\overrightarrow{v})\\ & =\frac{d}{dt}(\gamma m\overrightarrow{v})\\ & =\gamma m\frac{d\overrightarrow{v}}{dt}+m\overrightarrow{v}\frac{d\gamma }{dt}\\ & =m_{\text{rel}}\overrightarrow{a}+m{\gamma }^3(\overrightarrow{v}\cdot \overrightarrow{a})\overrightarrow{v}\end{array}$$ এখানে $m_{\text{rel}}\overrightarrow{a}$ এর সাথে আরেকটি এক্সট্রা টার্ম চলে আসছে। মানে বিশেষ শর্ত $(\overrightarrow{v}\cdot \overrightarrow{a}=0)$ আরোপ না করলে রিলেটিভিস্টিক 3-ফোর্স এর জন্য $\overrightarrow{F}=m_{\text{rel}}\overrightarrow{a}$ সত্যি হচ্ছে না। তেমনি গতিশক্তির বেলাতেও আপনারা চেক করে দেখতে পারেন, $E_k=\frac{1}{2}{m}_{\text{rel}}{v}^2$ সত্যি হয় না। এজন্য পদার্থবিদদেরা যারা প্রফেশনাল রিলেটিভিটিস্ট তাদের কাছে $m_{\text{rel}}$ এর অবতারণা অযৌক্তিক এবং এটার ব্যবহারের বিষয়ে তাঁরা নিরুৎসাহিত বহু বছর ধরেই।

সারকথা, স্পেশাল রিলেটিভিটিতে স্বীকৃত ভর আসলে একটাই। রেস্ট ভর বলতে যা বুঝতেন, সেটাই হল একমাত্র ভর। আর আপেক্ষিক গতি দ্বারা প্রভাবিত বা পরিবর্তিত হয় বস্তুর শক্তি, ভরবেগ; কিন্তু ভর নয়। কারণ এখানে বস্তুর ভর একটা ইনভ্যারিয়েন্ট (স্কেলার) রাশি হিসেবে সংজ্ঞায়িত যা নির্দেশ করে বস্তুর 4-ভরবেগের দৈর্ঘ্যকে$\text{(৩)}$ এবং বস্তুর নিজ ফ্রেমে তার মোট শক্তিকে$\text{(৬)}$।

যে প্রশ্ন দিয়ে আজকের লেখা শুরু করেছিলাম, সেটাতে ফিরি। বস্তুর বেগ আলোর বেগের সমান হতে পারে না কেন? ভর তো পরিবর্তন বা বৃদ্ধি পায় না, তাহলে? ভর বাড়ে না ঠিকই, কিন্ত বল প্রয়োগ করে বেগ বাড়ানোর সাথে সাথে বাড়তে থাকে জড়তা। কারণ এই জড়তার বৃদ্ধি কেবল ভরের উপর নয়; বস্তুর ভরবেগ, গতিশক্তি বৃদ্ধির উপরেও এটা নির্ভর করে। আর আলোর বেগের কাছাকাছি যেতে থাকলে বস্তুর নিজের বর্ধনশীল জড়তাই একসময় বস্তুটির বেগের বৃদ্ধিকে অসম্ভব করে তোলে।

লেখা আপাতত এখানে শেষ করছি আইনস্টাইনের উক্তি দিয়ে।

“It is not good to introduce the concept of the mass $M=m/\sqrt{1-\frac{v^2}{c^2}}$ of a moving body for which no clear definition can be given. It is better to introduce no other mass concept than the 'rest mass' $m$. Instead of introducing $M$, it is better to mention the expression for the momentum and energy of a body in motion.”

— আলবার্ট আইনস্টাইন, লিংকন বার্নেট-কে পাঠানো চিঠিতে, ১৯ জুন ১৯৪৮।

তথ্যসূত্র:

• L. Susskind, A. Friedman. Special Relativity and Classical Field Theory: The Theoretical Minimum. 2017.
• D. Fleisch. A Student's Guide to Vectors and Tensors. 2011.
• J. R. Taylor. Classical mechanics. 2005.
• S. Thornton, J. Marion. Classical Dynamics of Particles and Systems. 2004.
• A. Momen. Relativistic Mass: A Lost Cause. 2013 - Facebook Note.
• Why is relativistic mass considered a bad concept? - Quora.
• Z. K. Silagadze. Relativistic Mass and Modern Physics. 2014. arXiv: 1103.6281.
• E. Hecht. How Einstein Confirmed $E_0=m{c}^2$. 2011. DOI: 10.1119/1.3549223.
• E. Hecht. Einstein Never Approved of Relativistic Mass. 2009. DOI: 10.1119/1.3204111.
• L. B. Okun. Mass versus Relativistic and Rest Masses. 2009. DOI: 10.1119/1.3056168.
• P. M. Brown. On the Concept of Relativistic Mass. 2007. arXiv: 0709.0687.
• L. B. Okun. The Concept of Mass in the Einstein Year. 2006. arXiv: hep-ph/0602037.
• G. Oas. On the Abuse and Use of Relativistic Mass. 2005. arXiv: physics/0504110.
• L. B. Okun. The Concept of Mass. 1989. DOI: 10.1063/1.881171.
• C. G. Adler. Does mass really depend on velocity, dad? 1987. DOI: 10.1119/1.15314.